FABRIK Algorithm
In this post we’ll look at how to implement the FABRIK algorithm in 2D in JavaScript using the p5.js library for drawing. The Forward And Backward Reaching Inverse Kinematics (FABRIK) algorithm is a heuristic, iterative solver for the Inverse Kinematics problems.
What is the Goal?
Given a set of nodes that are connected together, we want to know how they should move when the end node is moved.
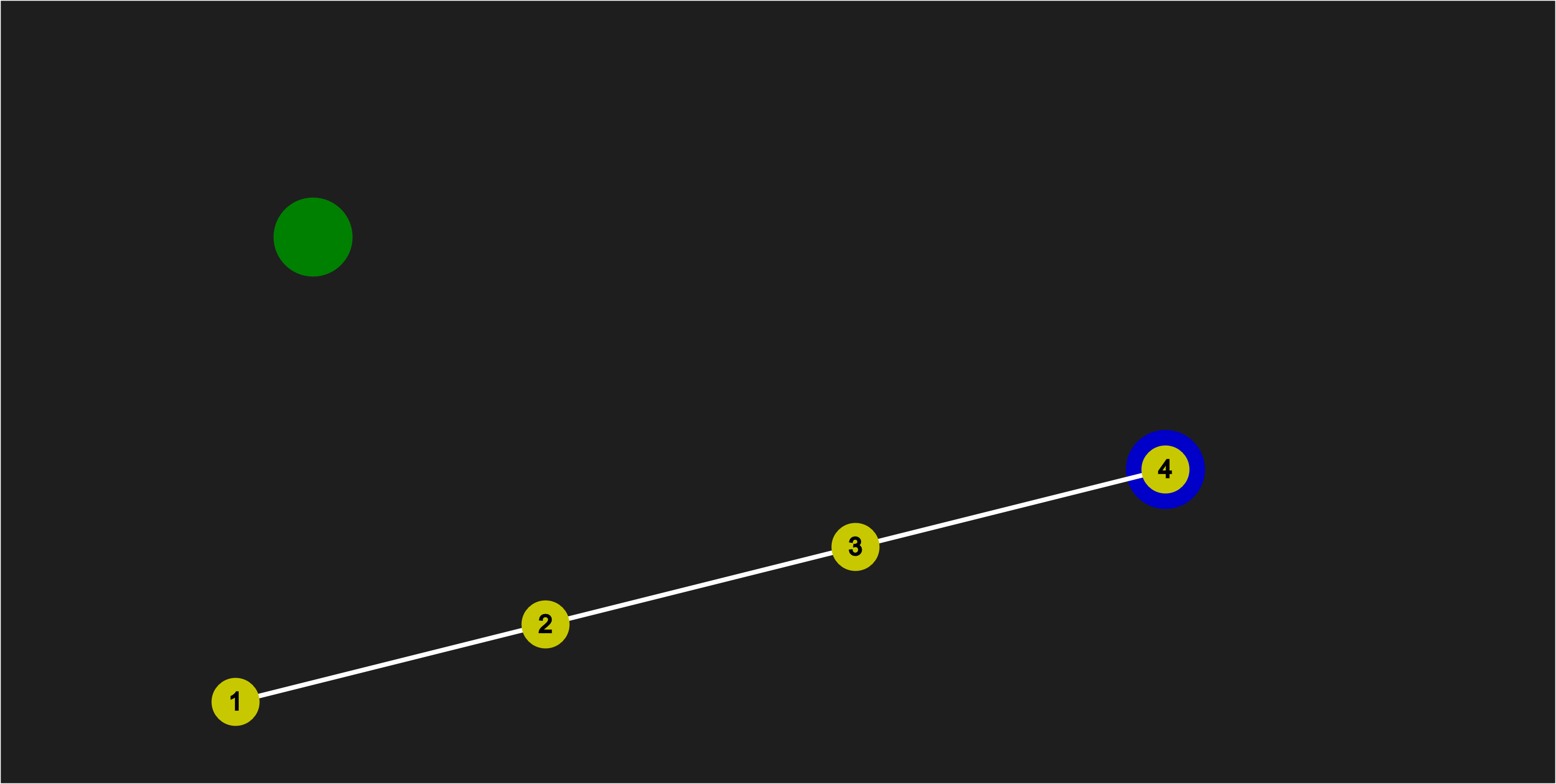
Starting Configuration
- The Blue Node is our fixed starting point.
- The Green Node is position where we want to move the end (left most) Node.
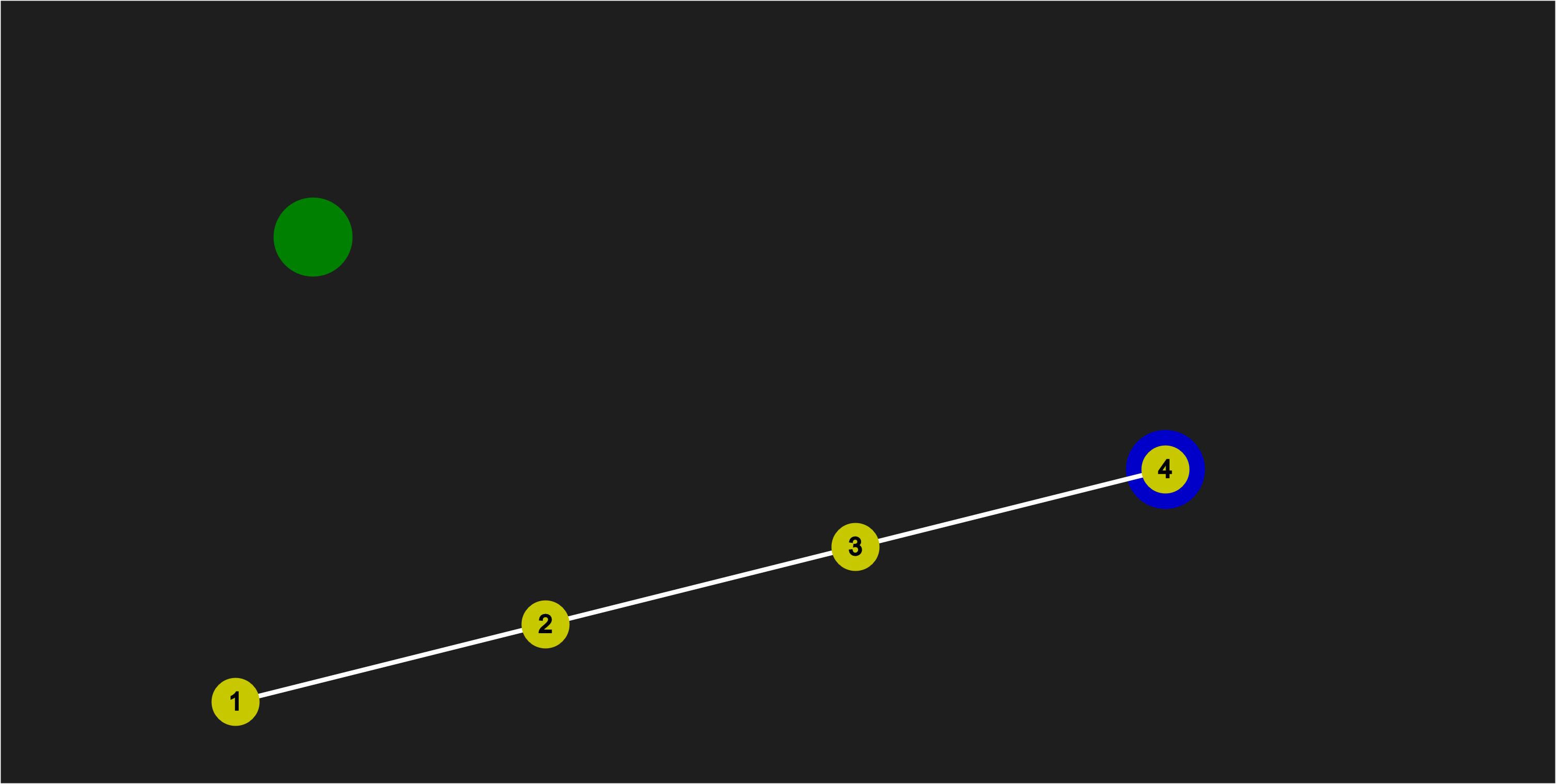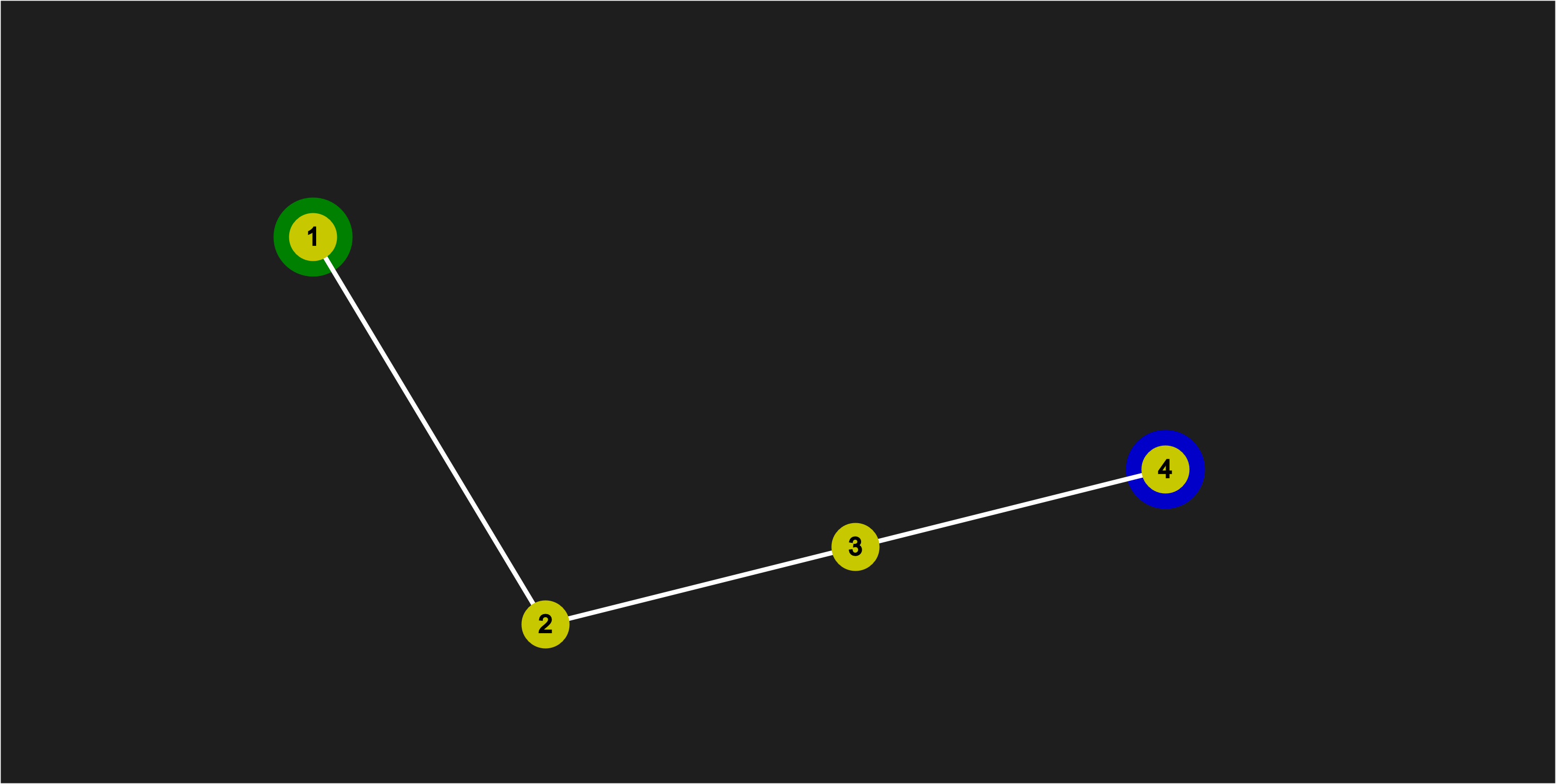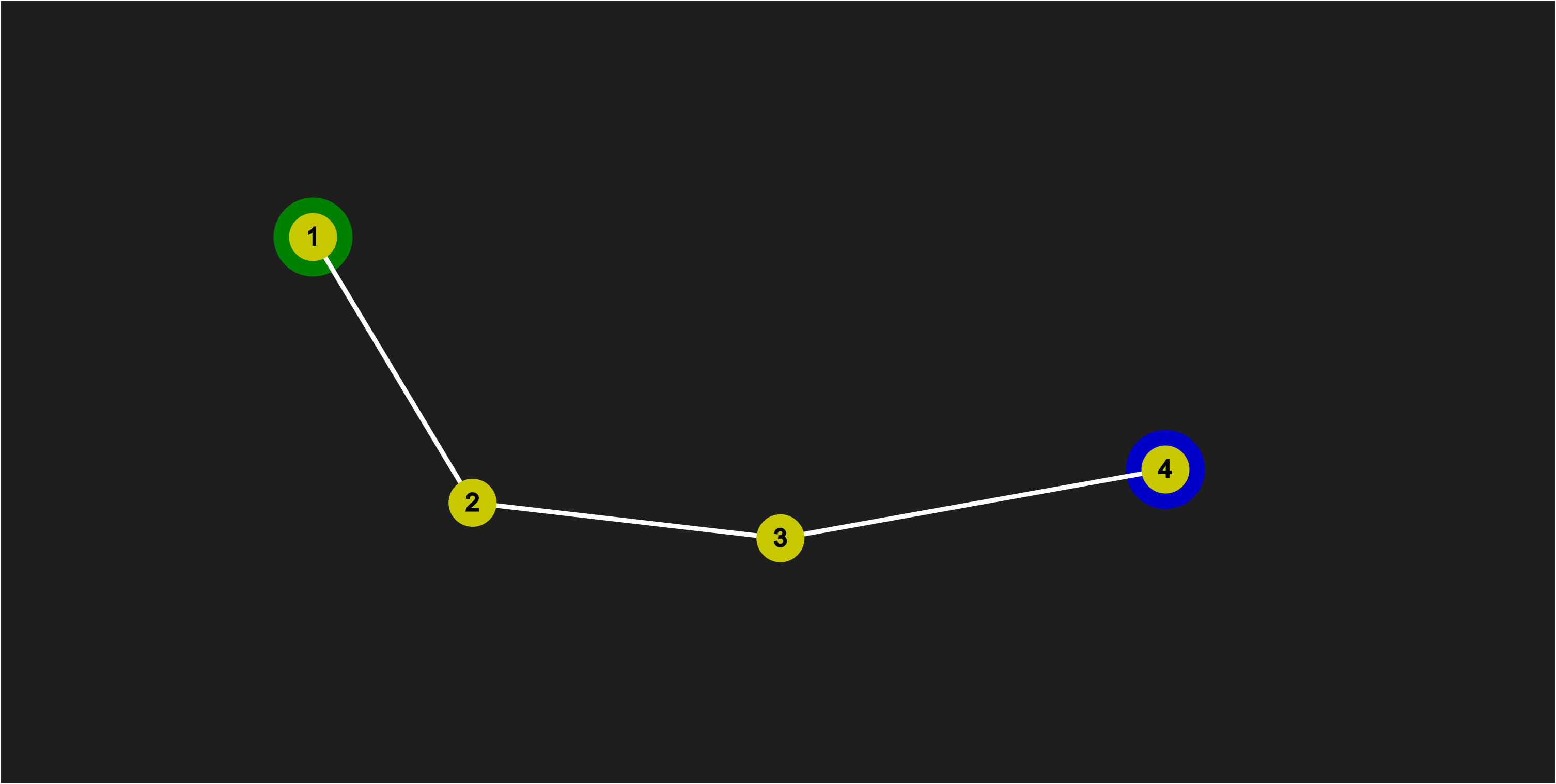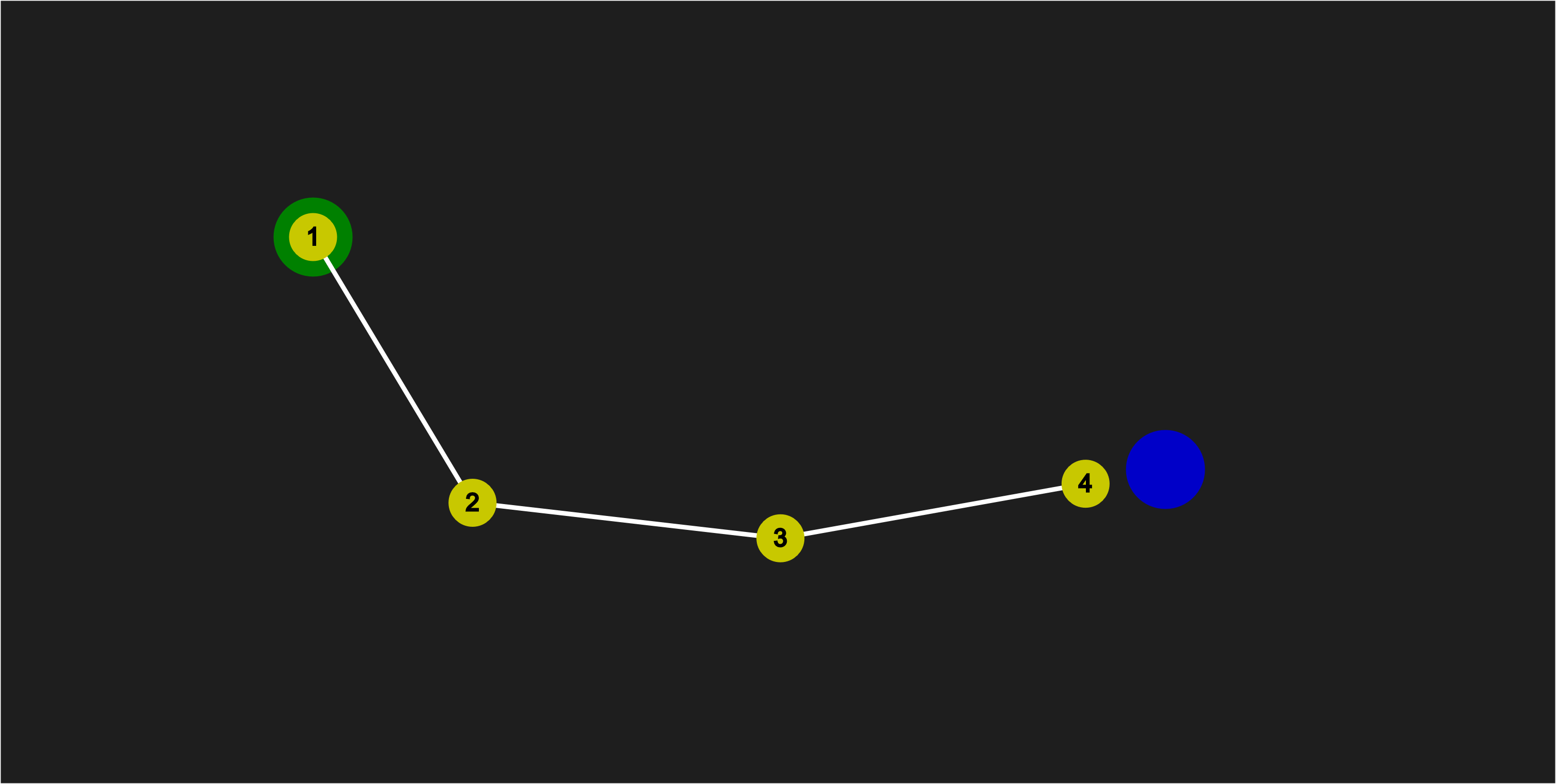
End Configuration
This is our end goal configuration which we want to calculate:
The Algorithm
The algorithm is iterative, so we will repeatable be doing the same steps until we reach our desired result. The steps of the algorithm are as follows:
- Move the first point desired location.
- Move the next point towards the previous so that it’s the correct distance away.
- Repeat Step 2 until all points are processed.
The above steps are a single iteration. Once a single iteration is complete, we do it again, but in the reverse order. So the point we finished on will be the starting point in the next iteration.
Step 1
Move the first point to the desired location (the Green Node):
Starting configuration
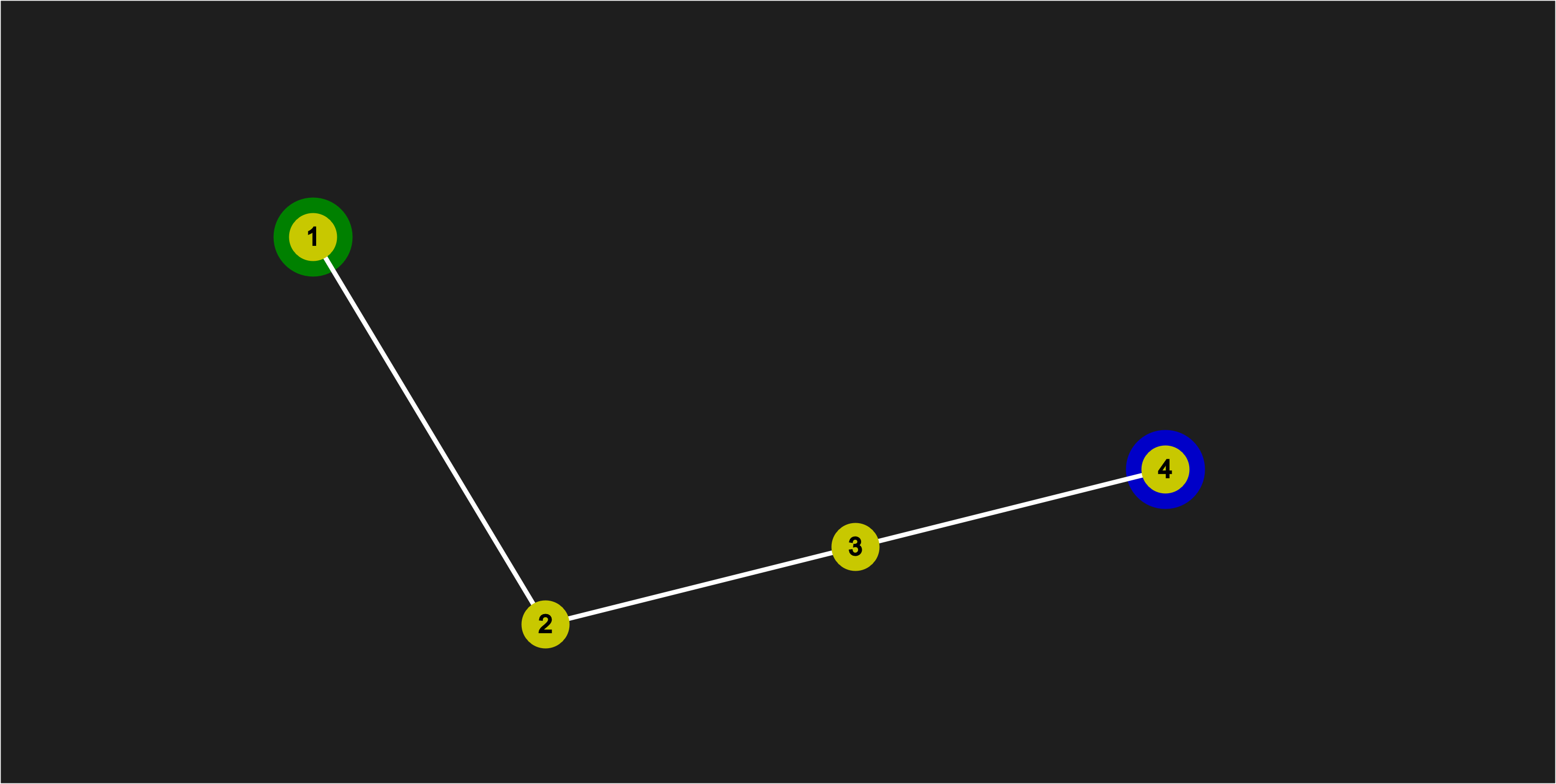Moving Point 1 to target location (Green Node)
Step 2
Move the next point towards the previous (in this case the first node) so it’s the correct distance away:
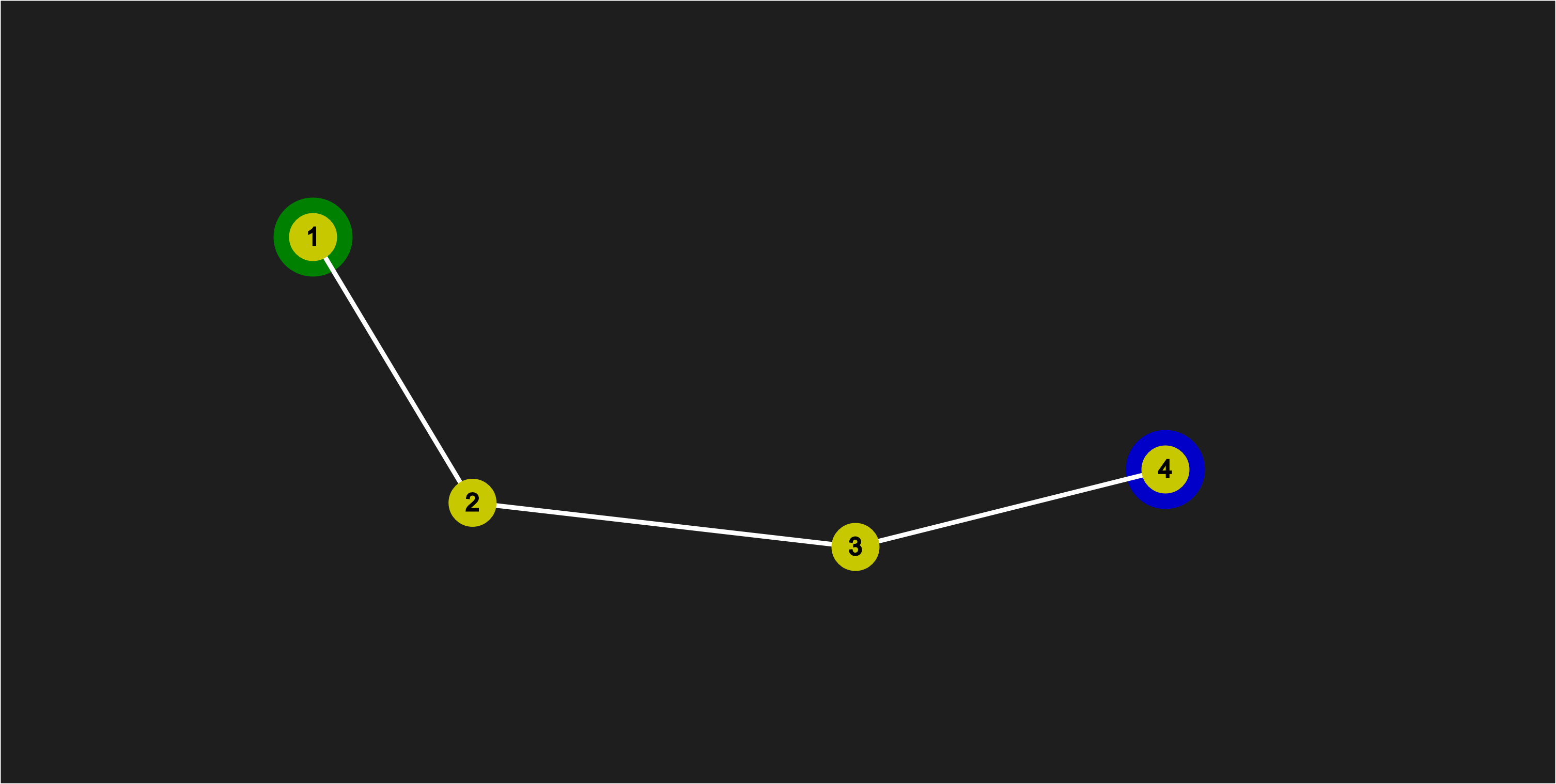Moving Point 2 towards Point 1
Step 3
Repeat Step 2 until all points are processed:
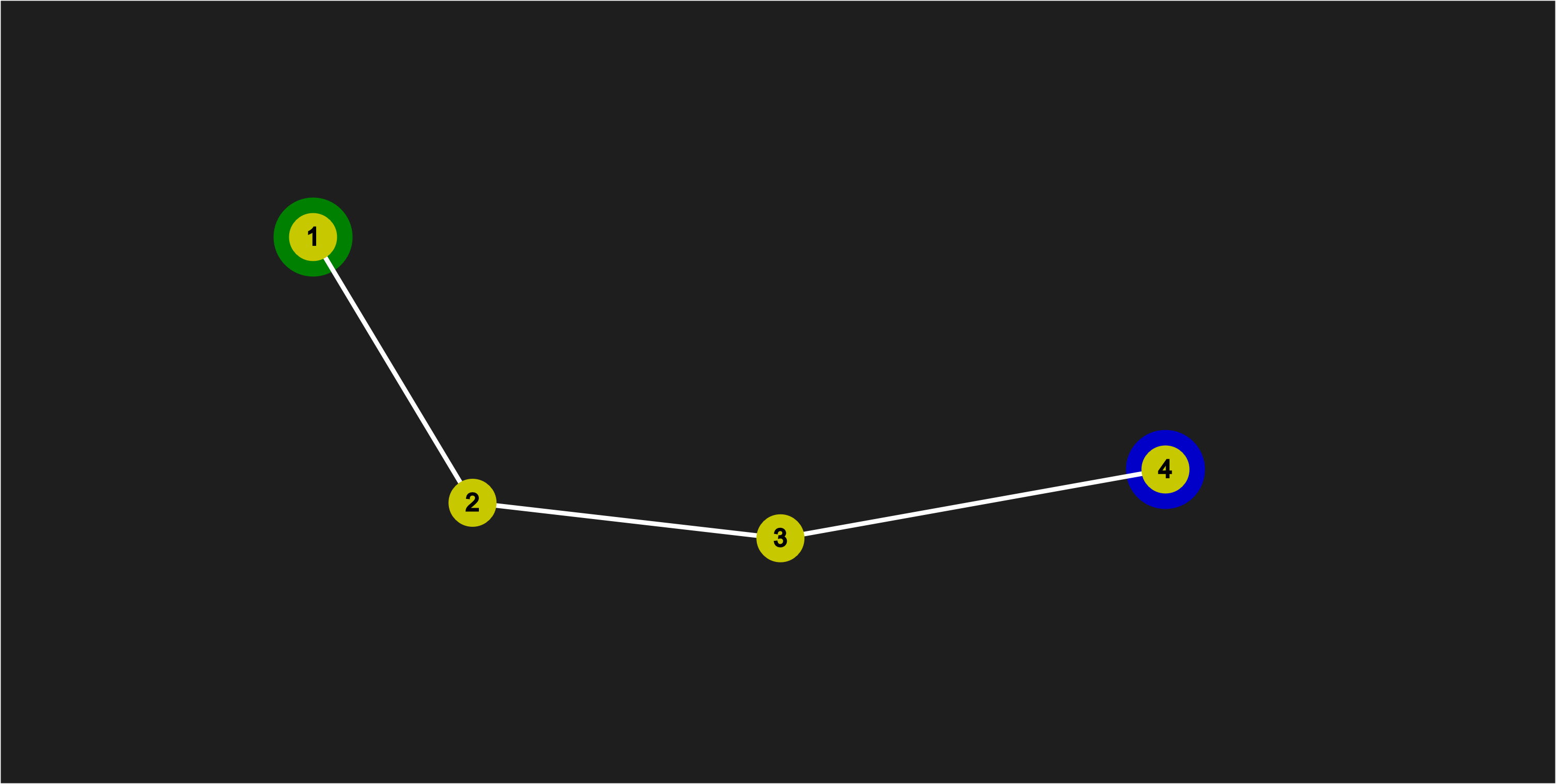Moving Point 3 towards Point 2
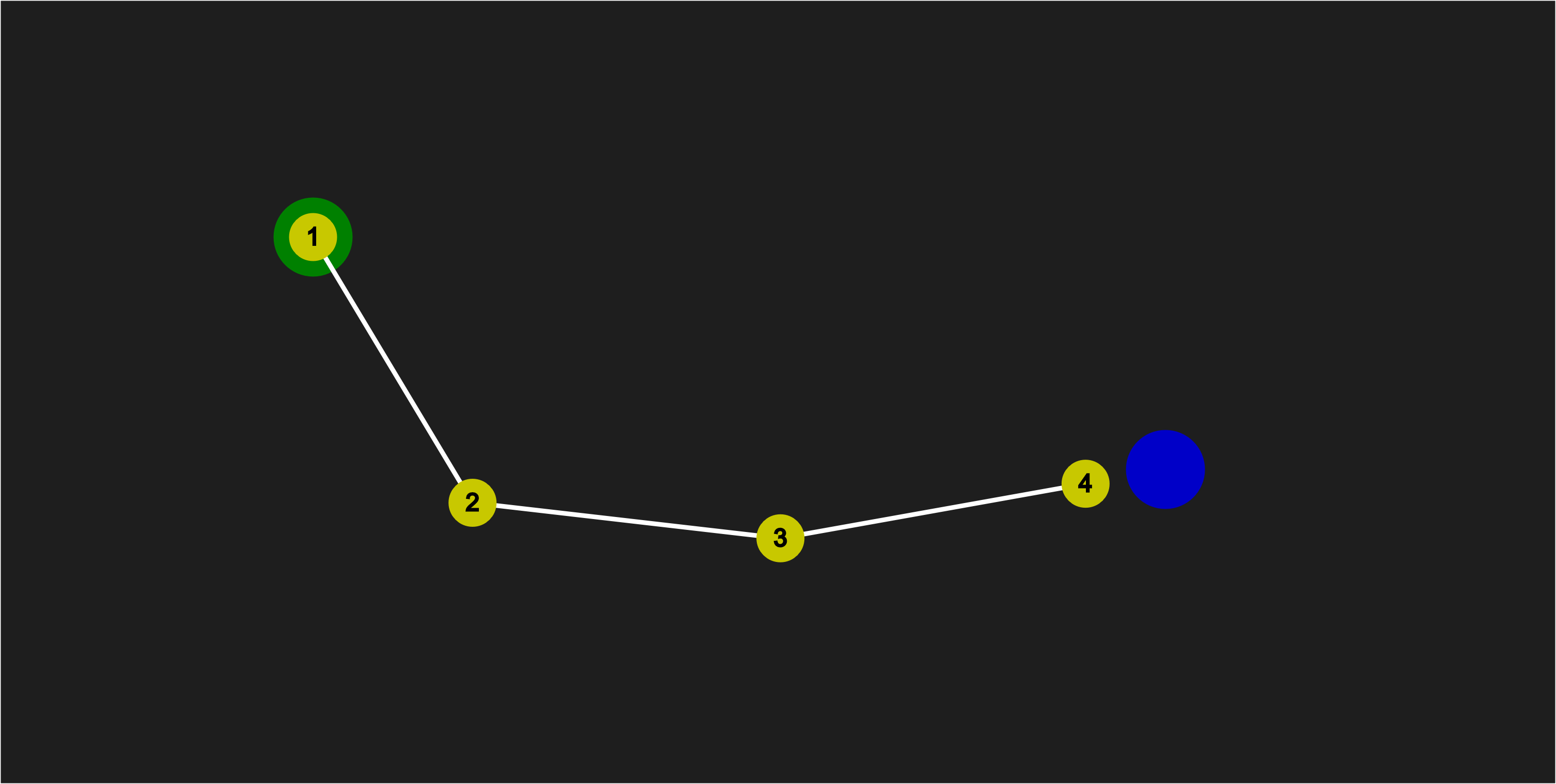Moving Point 4 towards Point 3
ITERATION COMPLETE
Full Single Iteration
Second Iteration
Notice that the order of the points has been reversed
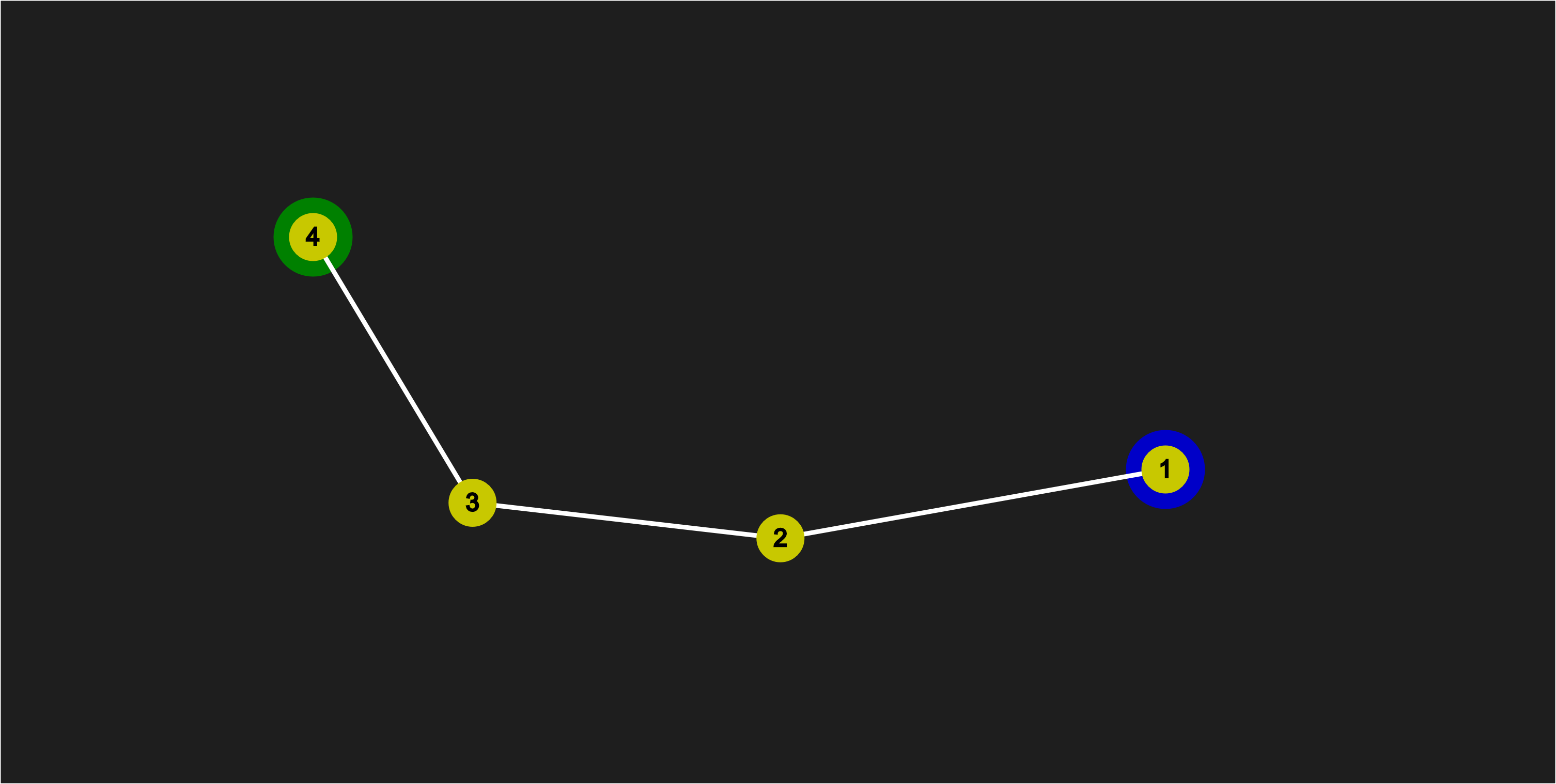Moving Point 1 to target location (Blue Node)
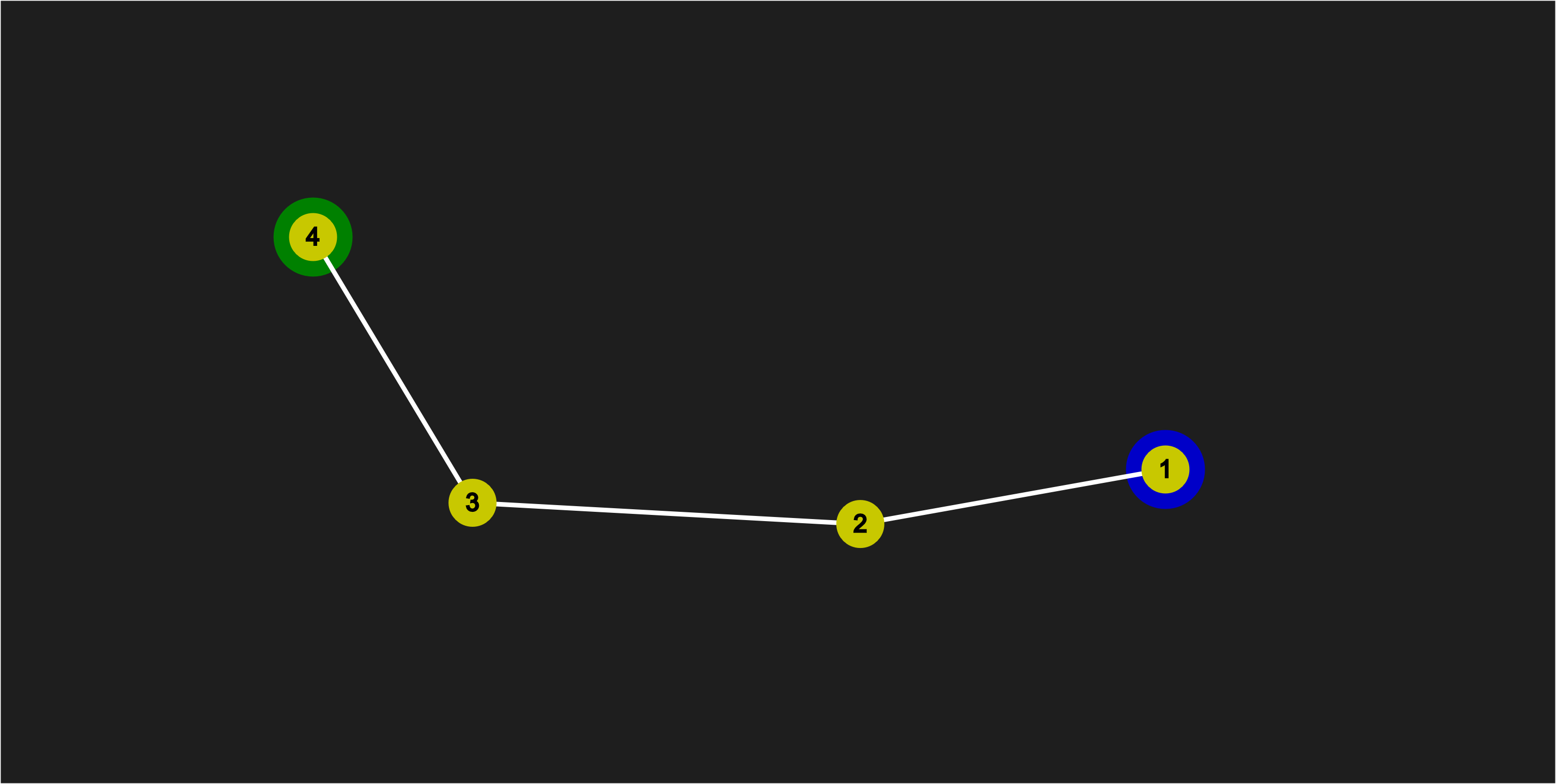Moving Point 2 towards Point 1
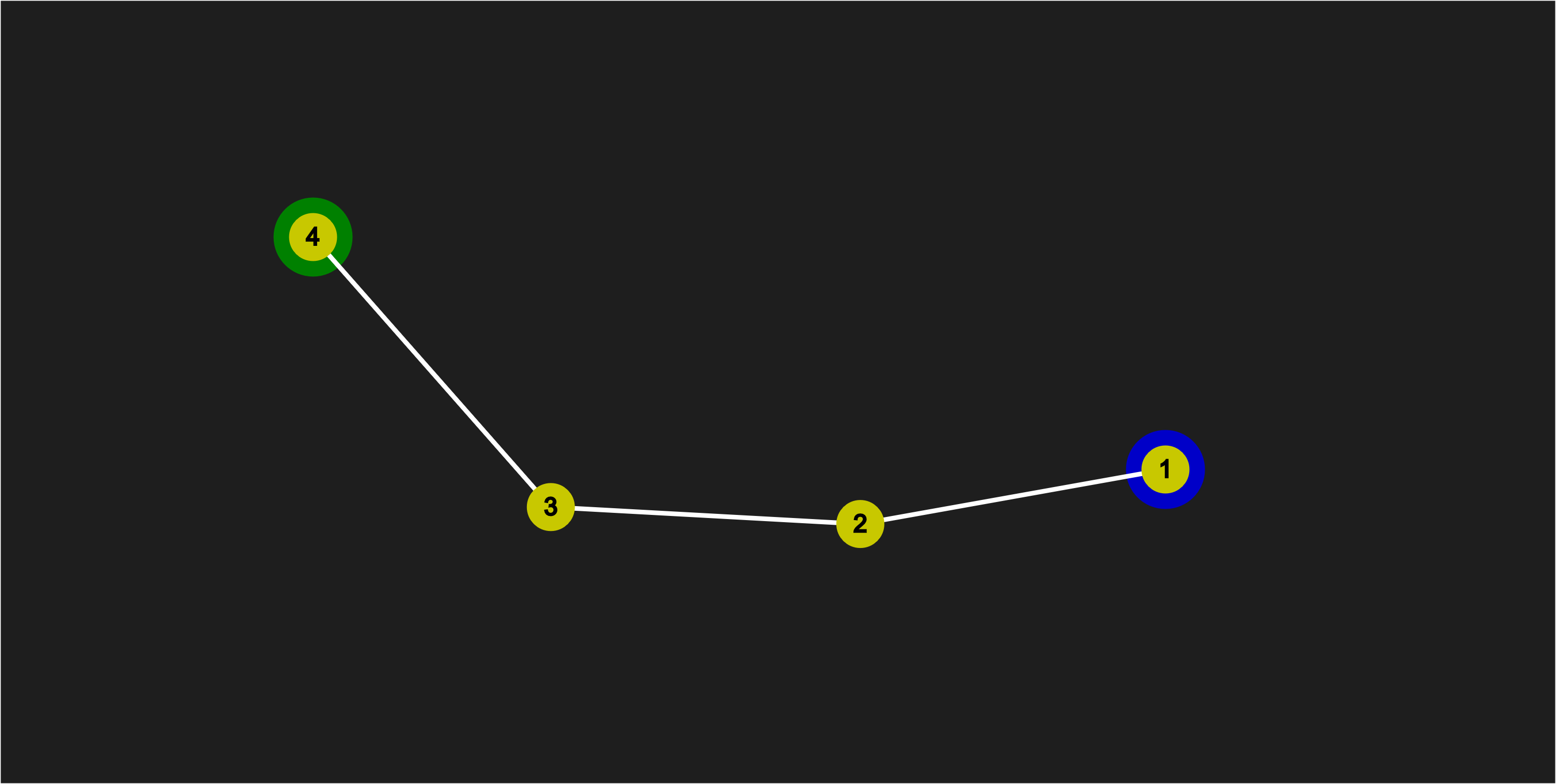Moving Point 3 towards Point 2
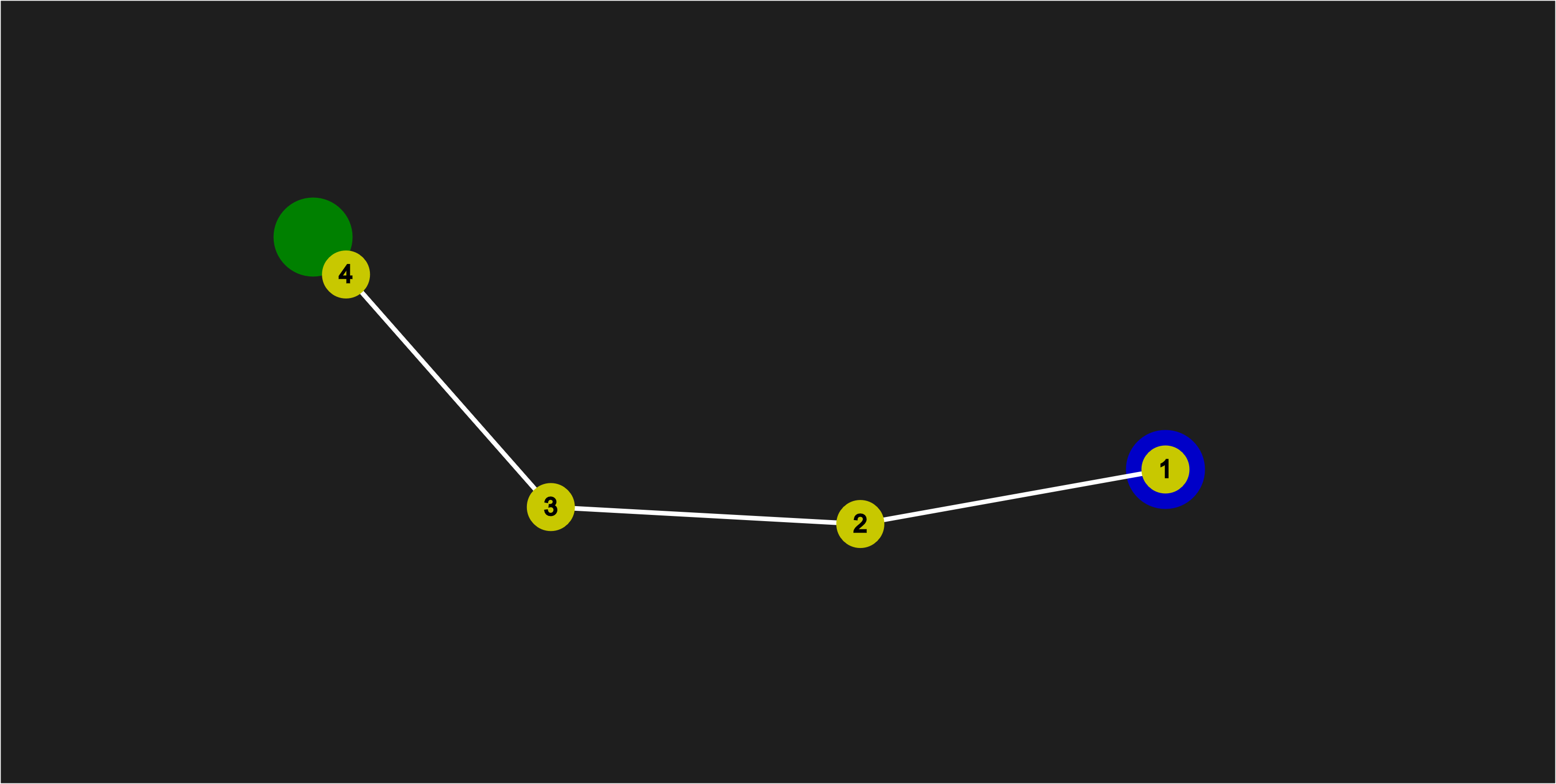Moving Point 4 towards Point 3
ITERATION COMPLETE
Completed
After performing 20 iterations (10 each way) we have the following result: