Maze Colouring with DFS and BFS

Maze colouring using BFS (Breadth-First Search) and DFS (Depth-First Search). For reference, the mazes in the below examples were generated using the Randomized Depth-First Search (Recursive Backtracking) and Aldous-Broder algorithms.

1. What are we Doing?
2. Colour Gradient
3. Small Static Example
4. Bigger Static Example
5. DFS (Depth-First Search) Animation
6. BFS (Breadth-First Search) Animation
7. Aldous-Broder Maze Generation

What are we Doing?

This post will visually demonstrate the difference of traversing through a maze using the BFS and DFS search methods. This post already assumes you know what both these methods are.

Colour Gradient

We’ll use the below colour gradient to show how far away cells are from the origin. The hue value of the cell will be scaled from 0 to 300, where 0 is the closest, and 300 is the furthest.

Closest Furthest Away

Small Static Example

The below maze is an example what we start with:

We then choose a random cell to be the starting point, then calculate how far away every cell in the maze is. We then colour the cell based on its distance using the colour gradient above.

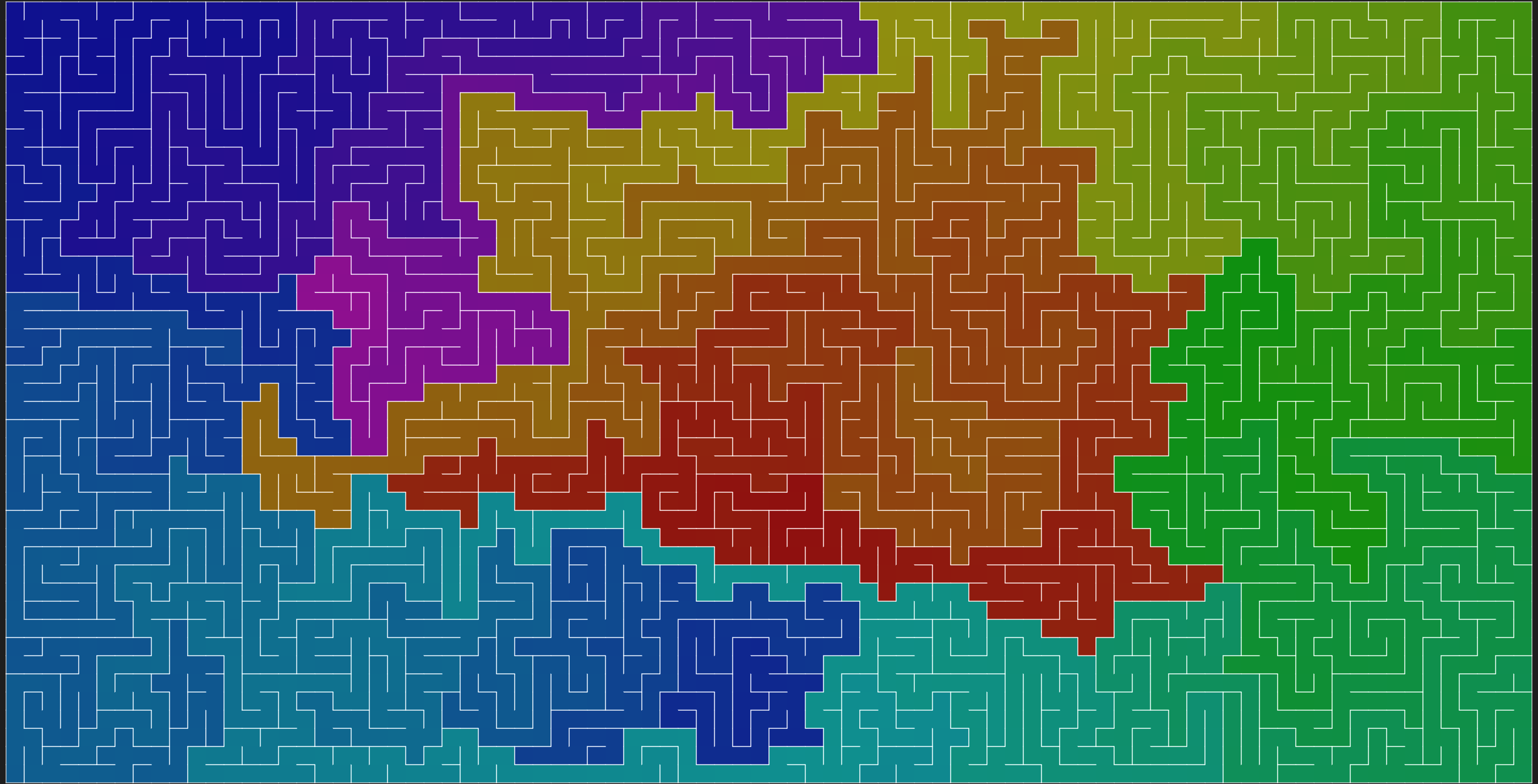
Bigger Static Example

If we increase the size of the maze, and remove the walls so the colours come through, we can get some interesting looking patterns:

DFS (Depth-First Search) Animation

The aboves images may look cool, but they don’t show any difference regarding the algorithm used (BFS or DFS). We need to see an animation of the construction to see the difference.

The following two videos will demonstrate the DFS traversal method. These mazes were generated using the Recursive Backtracking method.

Now on a bigger maze with no walls:

BFS (Breadth-First Search) Animation

The following two videos will demonstrate the BFS traversal method. These mazes were generated using the Recursive Backtracking method.

Now on a bigger maze with no walls:

Aldous-Broder Maze Generation

Recall that a spanning tree of a undirected graph is a tree that connects all the vertices of the graph, but contains no cycles. Each maze is one possible spanning tree of all the vertices in the graph.

All the previous mazes were generated using the Recursive Backtracking method. Mazes generated using this method tend to have long paths with less dead ends.

The Aldous-Broder method is different as it has a equal chance of generating each possible spanning tree (maze). The two mazes below were generated with this method.

Now on a bigger maze with no walls: